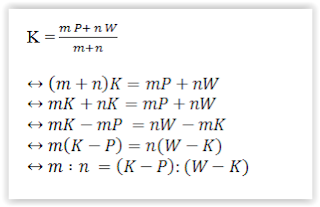Cara Kreatif menyelesaikan masalah rata-rata dengan metode perbandingan
Thursday, June 1, 2017
Edit
Cara Kreatif menyelesaikan masalah rata-rata dengan metode perbandingan
Disiplin ilmu matematika memiliki jangkauan yang luas akan tetapi satu dengan yang lain saling ada keterikatan dan tidak saling bertentangan seperti ketika kita hendak menyelesaikan masalah matematika. Satu permasalahan matematika tak harus menggunakan satu cara akan tetapi bisa menggunakan cara yang bermacam macam. Kita sebagai pendidik sudah seharunya untuk senantiasa mengembangkan ilmu untuk mencari cara atau ide kreatif dan membuat anak kreatif untuk menggunakan apa yang sudah dikuasai murid kita untuk digunakan dalam menyelesaikan masalah pada materi yang lain. Materi statistika terutama pada indikator menyelesaikan masalah rata-rata merupakan materi sulit bagi siswa terbukti dari hasil ujian nasional yang mengindikasikan bahwa materi statistika masalah rata-rata termasuk kedalam kategori yang sulit, dengan metode yang tepat maka akan sangat membantu ketuntasan belajar siswa. metode yang tepat maksudnya yang mudah dipahami , disenangi dan cepat pengerjaannya. Kesempatan ini kita akan belajar cara cerdas atau cara kreatif dalam menyelesaikan soal pemecahan masalah materi Aplikasi Rata-Rata dengan menggunakan konsep perbandingan.
Perhatikan Ilustrasi soal dibawah ini
Jika Rata-rata tinggi badan siswa pria dalam kelas adalah P dan banyak siswa pria m sedangkan rata-rata tinggi siswa wanita W serta n adalah banyak siswa wanita dan K rata-rata seluruh siswa.
Maka berlaku
Contoh soal
1. Rata-rata tinggi badan siswa pria 158 cm dan rata-rata tinggi siswa wanita 150 cm jika rata-rata seluruh siswa 153 cm dan banyaknya siswa dalam kelas itu 32 maka banyak siswa pria adalah...
a. 20 siswa c. 14 siswa
b. 18 siswa d. 12 siswa
2. Suatu kelas terdiri dari 40 siswa. Rata-rata tinggi siswa pria 150 cm dan rata-rata tinggi siswa wanita 140 cm. Jika rata-rata tinggi seluruh siswa 148 cm, maka banyak siswa Wanita adalah ....
A. 32 siswa C. 24 siswa
B. 28 siswa D. 8 siswa
Asik bukan penyelesaiannya. Tidak perlu menggunakan pemahaman yang sulit.
Demikian artikel tentang cara kreatif menyelesaikan masalah rata-rata dengan menggunakan model perbandingan.